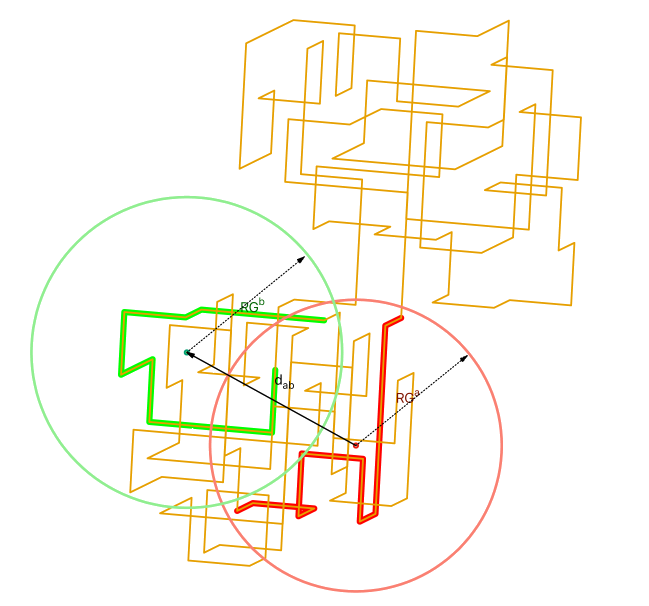
Inspired by recent advances in the chromosome capture techniques, a method is proposed to study the structural organization of systems of polymer rings with topological constraints. To this purpose, the system is divided into compartments and a simple condition is provided in order to determine if two compartments are in contact or not. Next, a set of contact matrices is defined that count how many times during a simulation a compartment 𝑎 was found in contact with a noncontiguous compartment 𝑏 in conformations with a given energy or temperature. Similar strategies based on correlation maps have been applied to the study of knotted polymers in the recent past. The advantage of the present approach is that is coupled with the Wang-Landau algorithm. Once the density of states is computed, it is possible to generate the contact matrices at any temperature. These matrices provide an information on the structure of knotted and linked polymers that is averaged over more than 10¹¹ conformations and visualized by means of color maps. The obtained color patterns allow us to identify the main properties of the structure of the system under investigation at any temperature. The method is applied to understand the structural rearrangements following the phase transitions of a knotted polymer ring and a circular polycatenane composed by four rings in a solution. The phase transitions are detected from the plots of the specific heat capacity with respect to the temperature. It is shown that the color maps have a finite number of patterns that can be clearly associated with the different phases of the investigated systems. The results agree with the available data coming from the plots of the observables and the close inspection of snapshots of the system taken at different steps of the simulations.

Download “Article preprint” contact_matrix.pdf – Downloaded 3 times – 3 MB

Download a copy of the manuscript (preprint version)