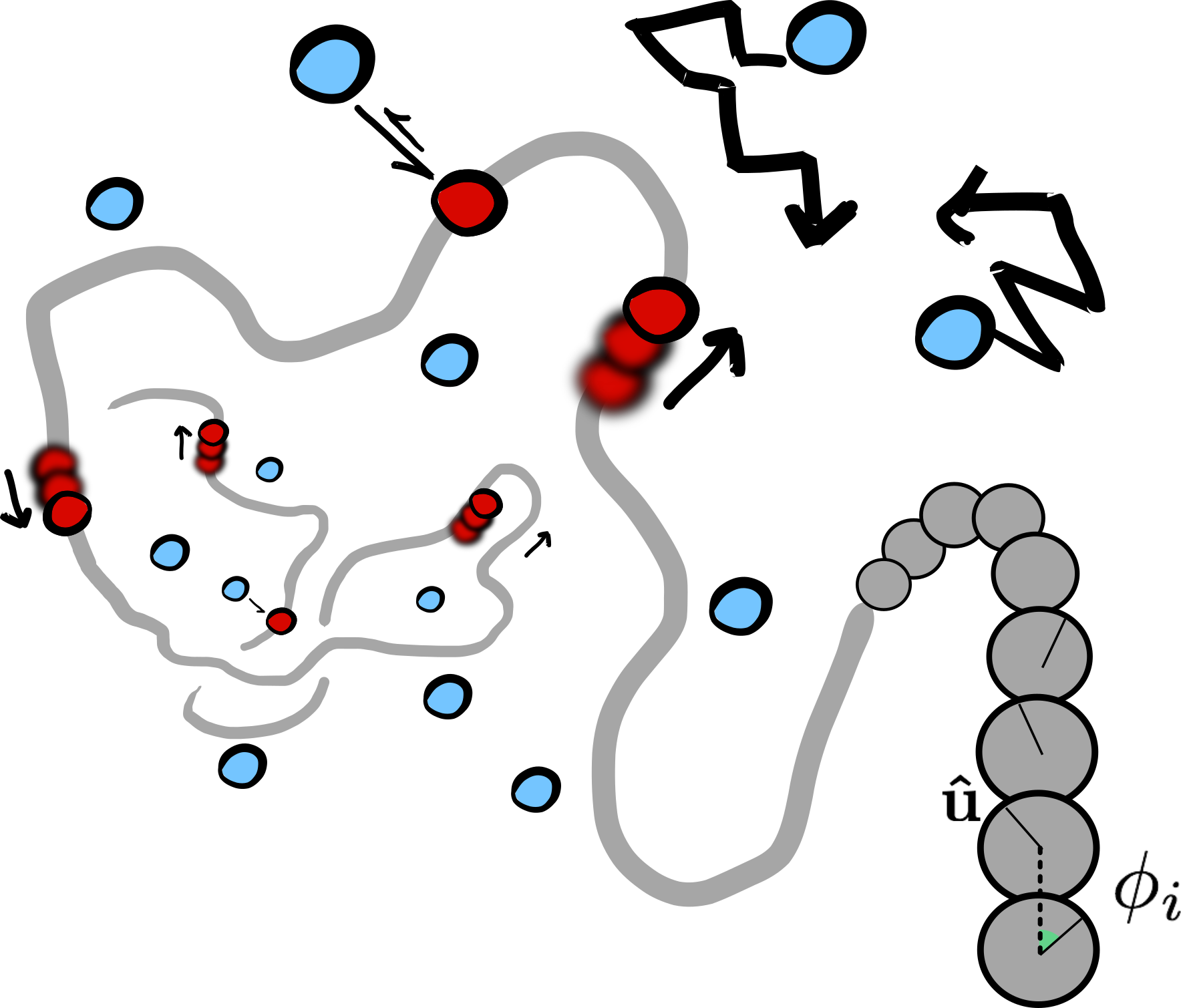
Molecular motors that work out-of-equilibrium are key elements for the viability of cells. Typical examples include myosin and kinesin motors, RNA and DNA polymerases, helicases and condensin. Although many of these protein complexes are biochemically well characterised, we are far from having a full understanding of their collective action in vivo. In some cases, the behaviour may be tuned by inter-motor interactions that are mediated by the substrate itself. We present a generic coarse-grained model to describe molecular motors acting on polymer substrates, mimicking, for example, RNA polymerase on DNA or kinesin on microtubules. We study, by means of Langevin dynamics simulations, the effect of the motor activity on both the conformational and dynamical properties of the substrate. We find that activity leads, in addition to the expected enhancement of polymer diffusion, to an effective reduction of its persistence length. We discover that this effective “softening” is a consequence of the emergence of double-folded branches, or hairpins, and that it can be tuned by changing the number of motors or the force they generate. Finally, we investigate the effect of the motors on the probability of knot formation. Counter-intuitively our simulations reveal that, even though at equilibrium a more flexible substrate would show an increased knotting probability, motor activity leads to a marked decrease in the occurrence of knotted conformations with respect to equilibrium.

Download “Article Preprint” Non-Equilibrium_Effects.pdf – Downloaded 386 times – 1 MB

Download a copy of the manuscript (preprint version)