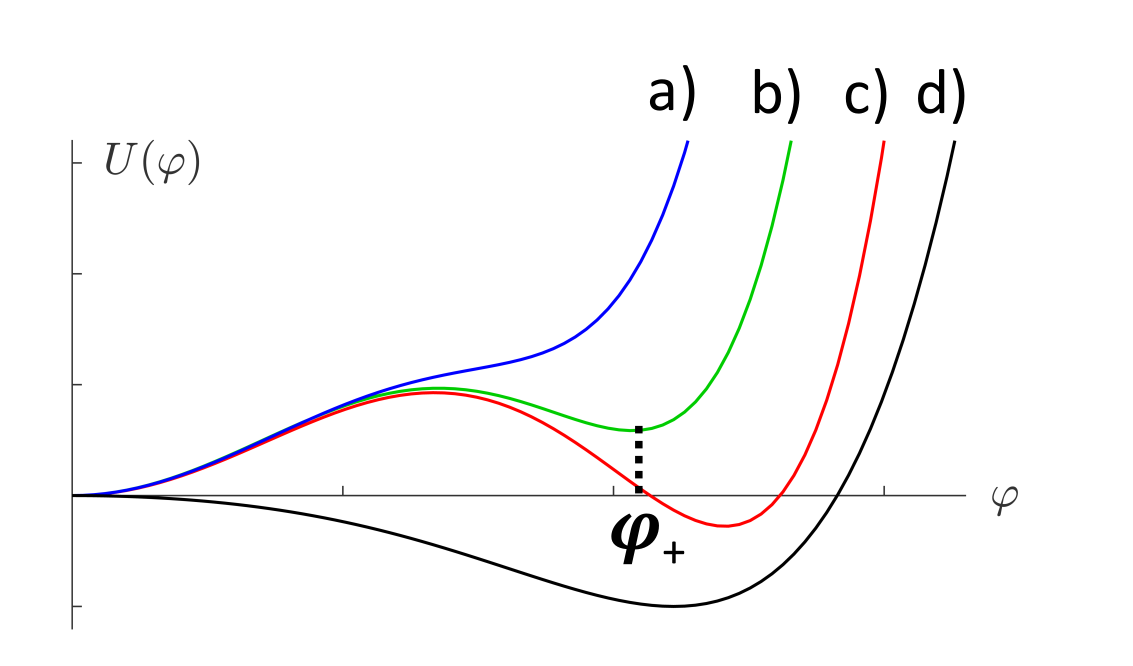
Classical Hamiltonian systems with conserved charges and those with constraints often describe dynamics on a pre-symplectic manifold. Here we show that a pre-symplectic manifold is also the proper stage to describe autonomous energy conserving Hamiltonian time crystals. We explain how the occurrence of a time crystal relates to the wider concept of spontaneously broken symmetries; in the case of a time crystal, the symmetry breaking takes place in a dynamical context. We then analyze in detail two examples of time crystalline Hamiltonian dynamics. The first example is a piecewise linear closed string, with dynamics determined by a Lie-Poisson bracket and Hamiltonian that relates to membrane stability. We explain how the Lie-Poisson brackets descents to a time crystalline pre-symplectic bracket, and we show that the Hamiltonian dynamics supports two phases; in one phase we have a time crystal and in the other phase time crystals are absent. The second example is a discrete Hamiltonian variant of the Q-ball Lagrangian of time dependent non-topological solitons. We explain how a Q-ball becomes a time crystal, and we construct examples of time crystalline Q-balls.
Download a copy of the manuscript (preprint version)