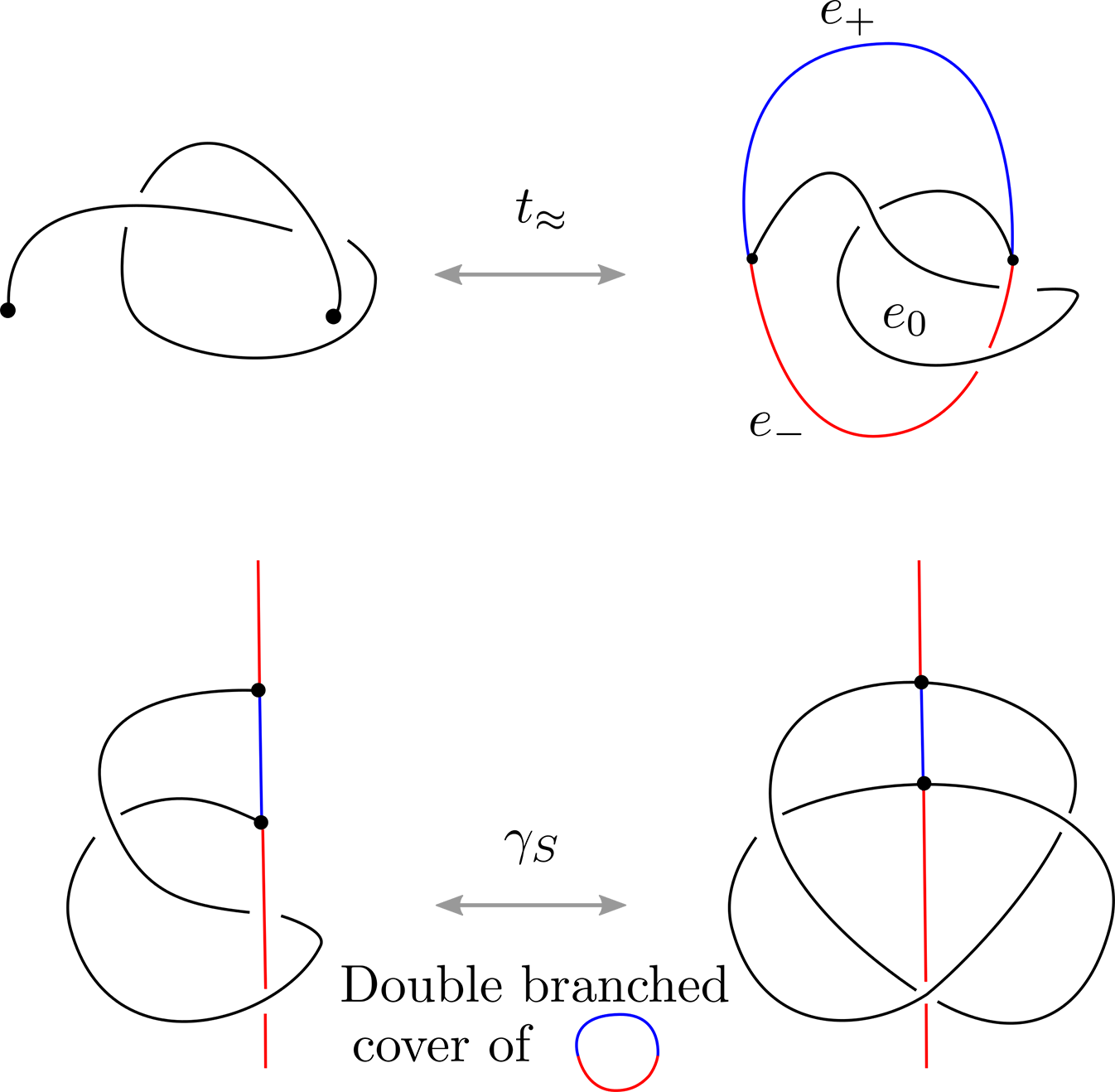
Recent studies classify the topology of proteins by analysing the distribution of their projections using knotoids. The approximation of this distribution depends on the number of projection directions that are sampled. Here we investigate the relation between knotoids differing only by small perturbations of the direction of projection. Since such knotoids are connected by at most a single forbidden move, we characterise forbidden moves in terms of equivariant band attachment between strongly invertible knots and of strand passages between θ-curves. This allows for the determination of the optimal sample size needed to produce a well approximated knotoid distribution. Based on that and on topological properties of the distribution, we propose a numerical measure for the determination of deeply knotted proteins that does not require the computationally expensive method of subchain analysis.

Download “Article preprint” fdistance_knotoids.pdf – Downloaded 182 times – 3 MB

Download a copy of the manuscript (preprint version)