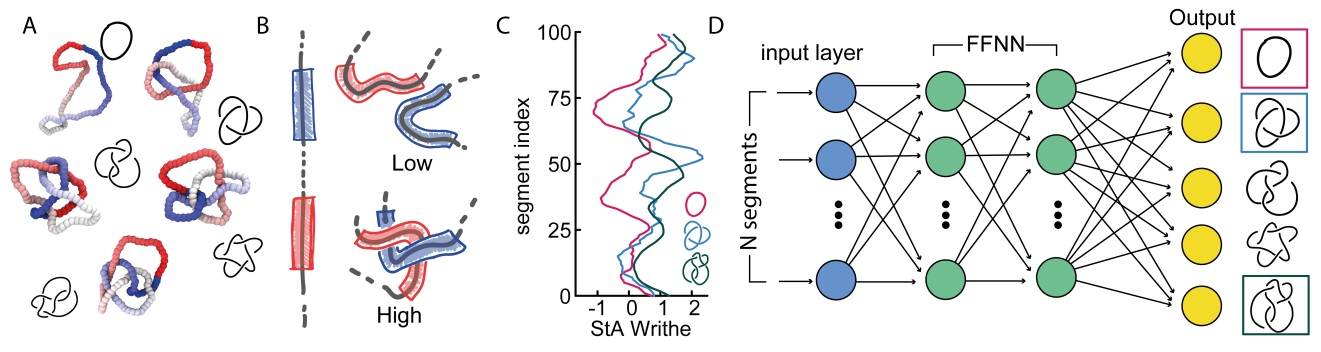
Knots are deeply entangled with every branch of science. One of the biggest open challenges in knot theory is to formalise a knot invariant that can unambiguously and efficiently distinguish any two knotted curves. Additionally, the conjecture that the geometrical embedding of a curve encodes information on its underlying topology is, albeit physically intuitive, far from proven. Here we attempt to tackle both these outstanding challenges by proposing a neural network (NN) approach that takes as input a geometric representation of a knotted curve and tries to make predictions of the curve’s topology. Intriguingly, we discover that NNs trained with a so-called geometrical “local writhe” representation of a knot can distinguish curves that share one or many topological invariants and knot polynomials, such as mutant and composite knots, and can thus classify knotted curves more precisely than some knot polynomials. Additionally, we also show that our approach can be scaled up to classify all prime knots up to 10-crossings with more than 95% accuracy. Finally, we show that our NNs can also be trained to solve knot localisation problems on open and closed curves. Our main discovery is that the pattern of “local writhe” is a potentially unique geometric signature of the underlying topology of a curve. We hope that our results will suggest new methods for quantifying generic entanglements in soft matter and even inform new topological invariants.

Download “Article” Geometric_Learning_Knot_Topology.pdf – Downloaded 97 times – 8 MB