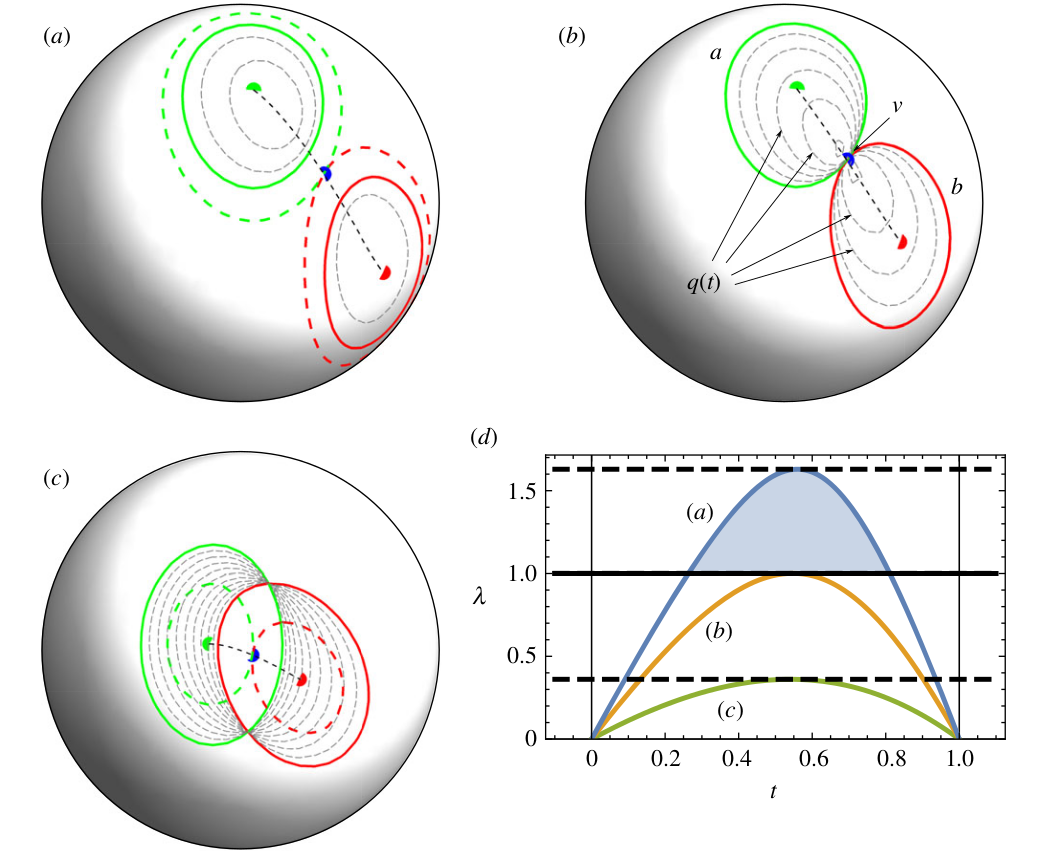
Various packing problems and simulations of hard and soft interacting particles, such as microscopic models of nematic liquid crystals, reduce to calculations of intersections and pair interactions between ellipsoids. When constrained to a spherical surface, curvature and compactness lead to non-trivial behaviour that finds uses in physics, computer science and geometry. A well-known idealized isotropic example is the Tammes problem of finding optimal non-intersecting packings of equal hard disks. The anisotropic case of elliptic particles remains, on the other hand, comparatively unexplored. We develop an algorithm to detect collisions between ellipses constrained to the two-dimensional surface of a sphere based on a solution of an eigenvalue problem. We investigate and discuss topologically distinct ways two ellipses may touch or intersect on a sphere, and define a contact function that can be used for construction of short- and long-range pair potentials.

Download “Article preprint” Measure_distance_overlap_between_two_arbitrary_ellipses.pdf – Downloaded 152 times – 1 MB