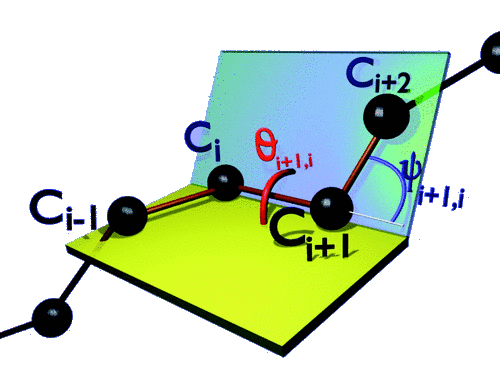
In this paper, a novel discrete algebra is presented which follows by combining the SU(2) Lie-Poisson bracket with the discrete Frenet equation. Physically, the construction describes a discrete piecewise linear string in R3. The starting point of our derivation is the discrete Frenet frame assigned at each vertix of the string. Then the link vector that connect the neighbouring vertices assigns the SU(2) Lie-Poisson bracket. Moreover, the same bracket defines the transfer matrices of the discrete Frenet equation which relates two neighbouring frames along the string. The procedure extends in a self-similar manner to an infinite hierarchy of Poisson structures. As an example, the first descendant of the SU(2) Lie-Poisson structure is presented in detail. For this, the spinor representation of the discrete Frenet equation is employed, as it converts the brackets into a computationally more manageable form. The final result is a nonlinear, nontrivial and novel Poisson structure that engages four neighbouring vertices.
Download “Article preprint” SU2_Algebra.pdf – Downloaded 215 times – 146 KB
Download a copy of the manuscript (preprint version)