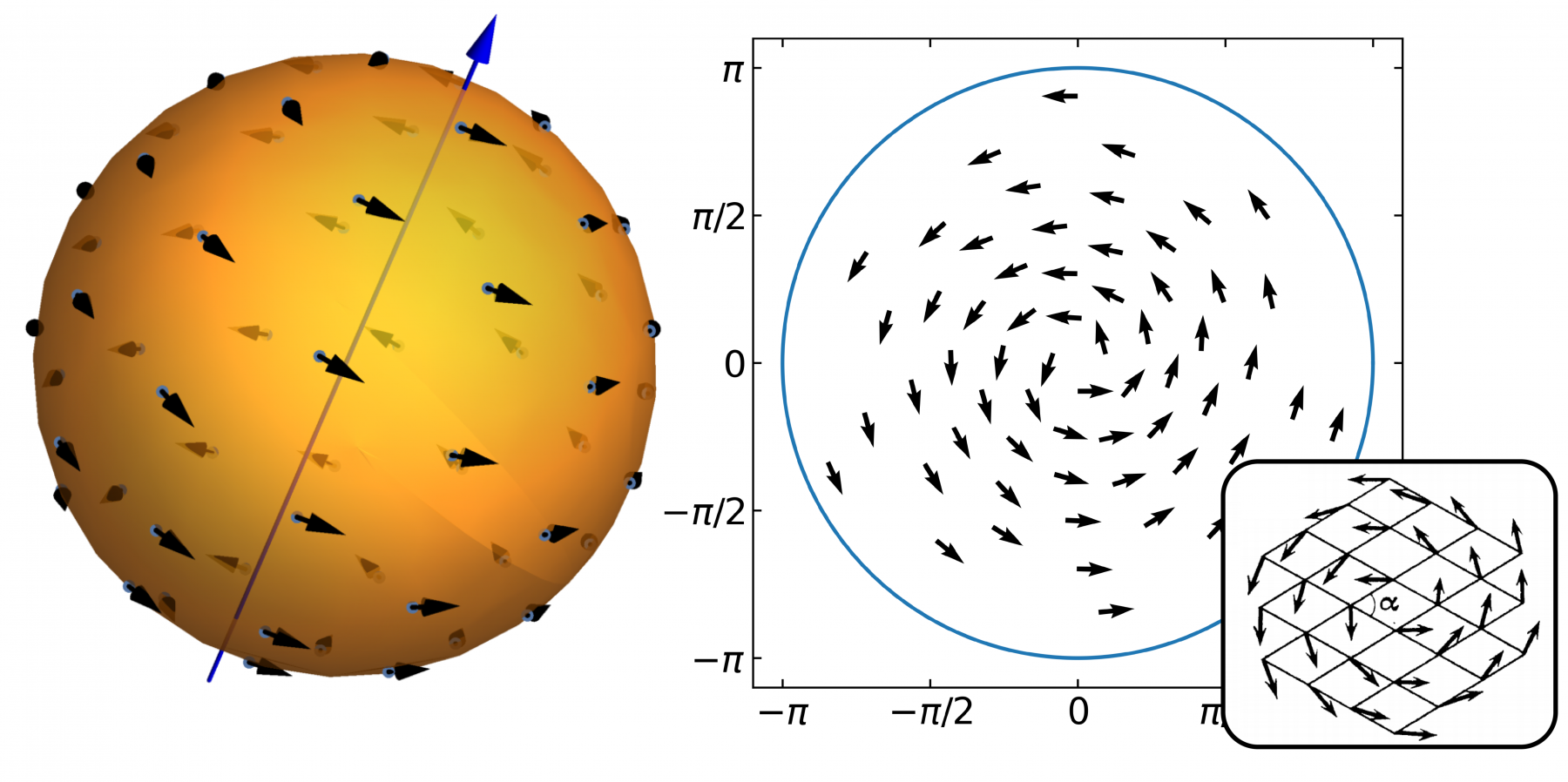
Arrangement of interacting particles on a sphere is historically a well known problem, however, ordering of particles with anisotropic interaction, such as the dipole-dipole interaction, has remained unexplored. We solve the orientational ordering of point dipoles on a sphere with fixed positional order with numerical minimization of interaction energy and analyze stable configurations depending on their symmetry and degree of ordering. We find that a macrovortex is a generic ground state, with various discrete rotational symmetries for different system sizes, while higher energy metastable states are similar, but less ordered. We observe orientational phase transitions and hysteresis in response to changing external field both for the fixed sphere orientation with respect the field, as well as for a freely-rotating sphere. For the case of a freely rotating sphere, we also observe changes of the symmetry axis with increasing field strength.
Download a copy of the manuscript (preprint version)