Understanding how unconcatenated and unlinked ring polymers pack in concentrated solutions and melt is a long-standing, puzzling problem in polymer physics. Theoretical considerations corroborated by computer simulations have suggested that rings fold into double-folded conformations on randomly branched primitive trees.
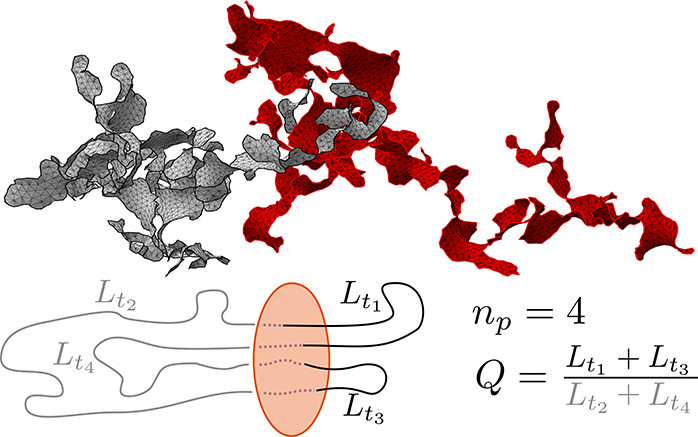
In this work, we challenge this picture. Motivated by recent theoretical evidence that rings should display extensive intermingling in the form of long-lived topological constraints or threadings, here we employ the concept of ring minimal surface to measure the extent of threadings in solutions of ring polymers constructed in two different manners: (1) by the double-folded branched polymer model and (2) by brute-force molecular dynamics computer simulations. If pictures (1) and (2) are equivalent, the minimal surface analysis would not be able to distinguish between the two.
Instead, our results show that the double-folded ring polymers are significantly less threaded compared to their MD-equilibrated counterparts. Second, we demonstrate that threadings form through a slow process whose characteristic time-scale is of the same order of magnitude as that of the diffusion of the rings in solution. These findings are robust, being based on universal (model-independent) observables as the average fraction of threaded length or the total penetrations between close-by rings and the corresponding distribution functions.
Download a copy of the manuscript (preprint version)