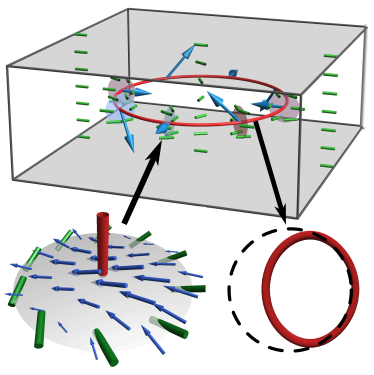
We describe the flows and morphological dynamics of topological defect lines  and loops in three-dimensional active nematics and show, using theory and  numerical modeling, that they are governed by the local profile of the orientational order surrounding the defects. Analyzing a continuous span of defect loop profiles, ranging from radial and tangential twist to wedge ±1/2 profiles, we show that the distinct geometries can drive material flow perpendicular or along the local defect loop segment, whose variation around a closed loop can lead to net loop motion, elongation, or compression of shape, or buckling of the loops. We demonstrate a correlation between local curvature and  the local orientational profile of the defect loop, indicating dynamic coupling between geometry and topology. To address the general formation of defect  loops in three dimensions, we show their creation via bend instability from  different initial elastic distortions.

Download “Article” Three-Dimensional_Active_Defect_Loops.pdf – Downloaded 235 times – 2 MB