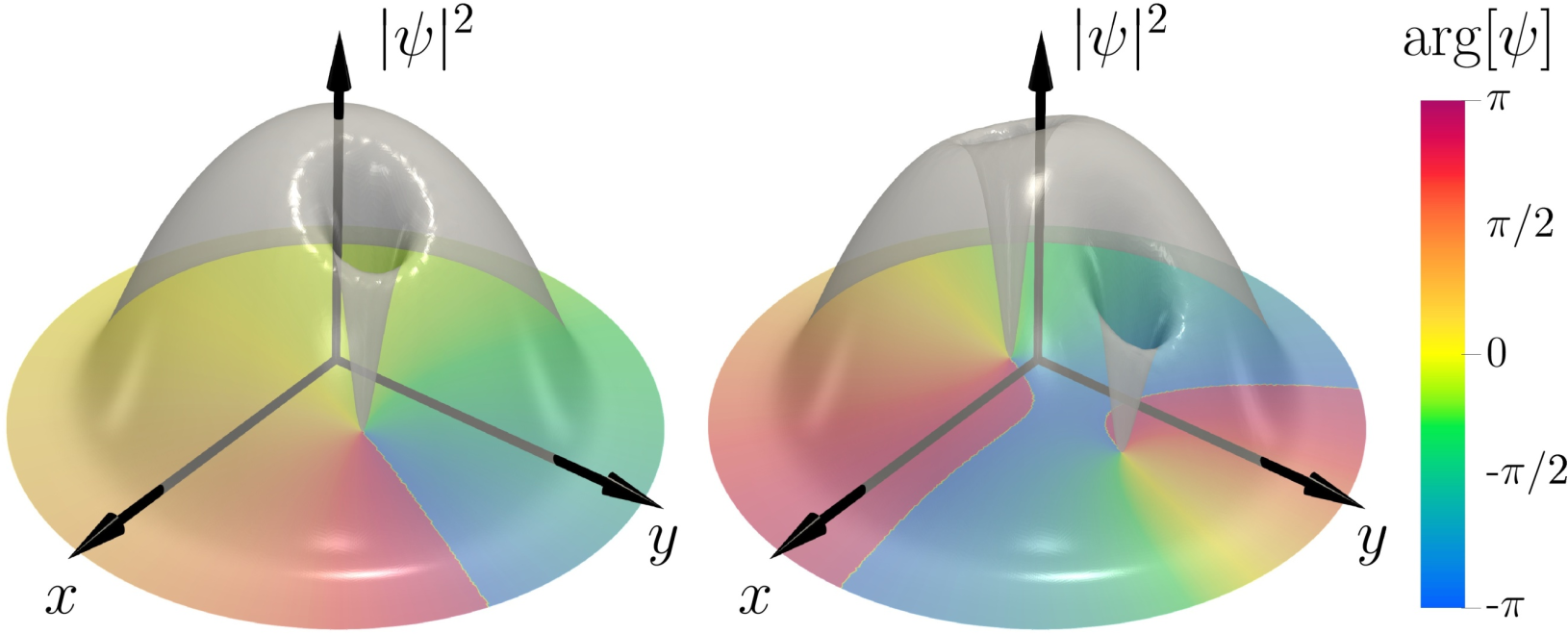
Vortices in a Bose-Einstein condensate are modelled as spontaneously symmetry breaking minimum energy solutions of the time dependent Gross-Pitaevskii equation, using the method of constrained optimization. In a non-rotating axially symmetric trap, the core of a single vortex precesses around the trap center and, at the same time, the phase of its wave function shifts at a constant rate. The precession velocity, the speed of phase shift, and the distance between the vortex core and the trap center, depend continuously on the value of the conserved angular momentum that is carried by the entire condensate.
In the case of a symmetric pair of identical vortices, the precession engages an emergent gauge field in their relative coordinate, with a flux that is equal to the ratio between the precession and shift velocities
Download “Article” Vortex_precession_and_exchange.pdf – Downloaded 285 times – 3 MB
Download a copy of the manuscript