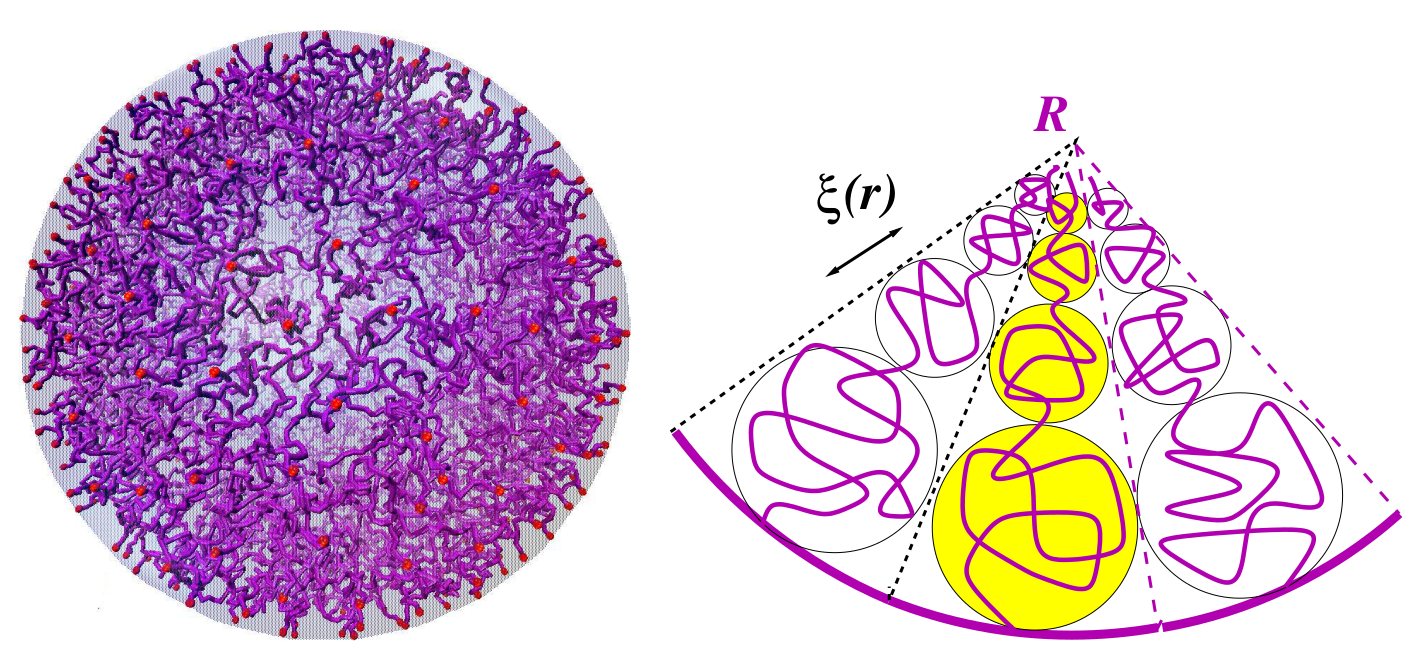
The structure and scaling properties of inwardly curved polymer brushes, tethered under good solvent conditions to the inner surface of spherical shells like membranes and vesicles, are studied by extensive Molecular Dynamics simulations and compared with earlier scaling and Self-Consistent Field Theory (SCFT) predictions for different molecular weight of the polymer chains N and grafting density σ g in the case of strong surface curvature, R⁻¹ . We examine the variation of the critical radius R ∗ (σ_g ), separating the regimes of weak concave brushes and compressed brushes, predicted earlier by Manghi et al. [Eur. Phys. J. E 5, 519 (2001)] as well as various structural proper-ties as the radial monomer- and chain-end density profiles, orientation of bonds, brush thickness, etc. The impact of chain stiffness, κ, on concave brush conformations is briefly considered too. Eventually we present the radial profiles of local pressure normal, P_N , and tangential, P_T , to the grafting shell, the surface tension, γ(σ_g ), for soft and semi-rigid brushes, and find a new scaling relationship P_N(R) ∝ σ_g⁴ , independent of the degree of chain stiffness.

Download “Article preprint” Concave_brushes.pdf – Downloaded 96 times – 26 MB

Download a copy of the manuscript (preprint version)