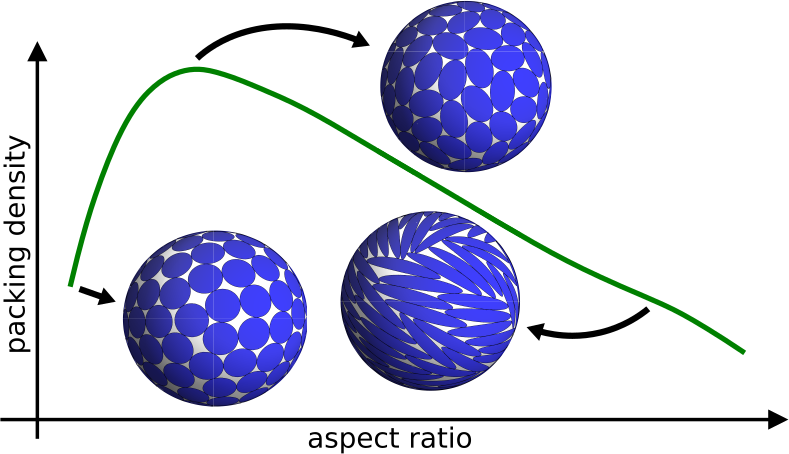
Packing problems are abundant in nature and have been researched thoroughly both experimentally and in numerical models. In particular, packings of anisotropic, elliptical particles often emerge in models of liquid crystals, colloids, and granular and jammed matter. While most theoretical studies on anisotropic particles have thus far dealt with packings in Euclidean geometry, there are many experimental systems where anisotropically-shaped particles are confined to a curved surface, such as Pickering emulsions stabilized by ellipsoidal particles or protein adsorbates on lipid vesicles. Here, we study random close packing configurations in a two-dimensional model of spherical geodesic ellipses. We focus on the interplay between finite-size effects and curvature that is most prominent at smaller system sizes. We demonstrate that on a spherical surface, monodisperse ellipse packings are inherently disordered, with a non-monotonic dependence of both their packing fraction and the mean contact number on the ellipse aspect ratio, as has also been observed in packings of ellipsoids in both 2D and 3D flat space. We also point out some fundamental differences with previous Euclidean studies and discuss the effects of curvature on our results. Importantly, we show that the underlying spherical surface introduces frustration and results in disordered packing configurations even in systems of monodispersed particles, in contrast to the 2D Euclidean case of ellipse packing. This demonstrates that closed curved surfaces can be effective at introducing disorder in a system and could facilitate the study of monodispersed random packings.

Download “Article” Dense_packings_geodesic_hard_ellipses_sphere.pdf – Downloaded 97 times – 1 MB