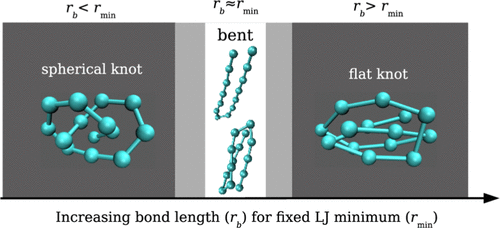
Semiflexible polymer models are widely used as a paradigm to understand structural phases in biomolecules including folding of proteins. Since stable knots are not so common in real proteins, the existence of stable knots in semiflexible polymers has not been explored much. Here, via extensive replica exchange Monte Carlo simulation we investigate the same for a bead-stick and a bead-spring homopolymer model that covers the whole range from flexible to stiff. We establish the fact that the presence of stable knotted phases in the phase diagram is dependent on the ratio rb/rmin where rb is the equilibrium bond length and rmin is the distance for the strongest nonbonded contacts. Our results provide evidence for both models that if the ratio rb/rmin is outside a small window around unity then depending on the bending stiffness one always encounters stable knotted phases along with the usual frozen and bent-like structures at low temperatures. These findings prompt us to conclude that knots are generic stable phases in semiflexible polymers.
Download a copy of the manuscript (preprint version)