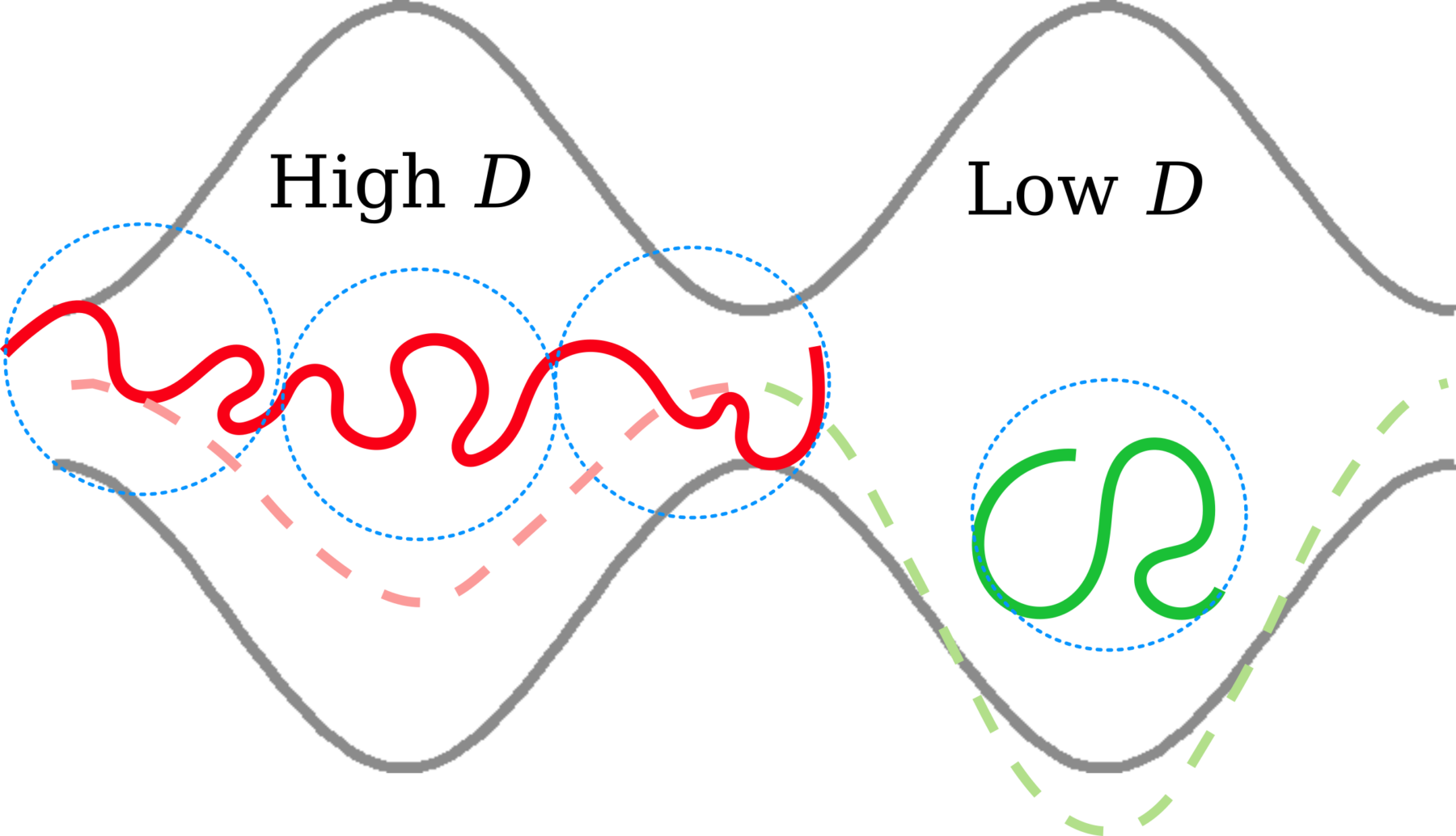
Polymers confined in corrugated channels, i.e., channels of varying amplitude, display multiple local maxima and minima of the diffusion coefficient upon increasing their degree of polymerization N. We propose a theoretical effective free energy for linear polymers based on a Fick-Jacobs approach. We validate the predictions against numerical data, obtaining quantitative agreement for the effective free energy, the diffusion coefficient, and the mean first passage time. Finally, we employ the effective free energy to compute the polymer lengths N_min at which the diffusion coefficient presents a minimum: we find a scaling expression that we rationalize with a blob model. Our results could be useful to design porous adsorbers, that separate polymers of different sizes without the action of an external flow.

Download “Article preprint” Nonmonotonous_translocation_time.pdf – Downloaded 110 times – 431 KB

Download a copy of the article (preprint version)