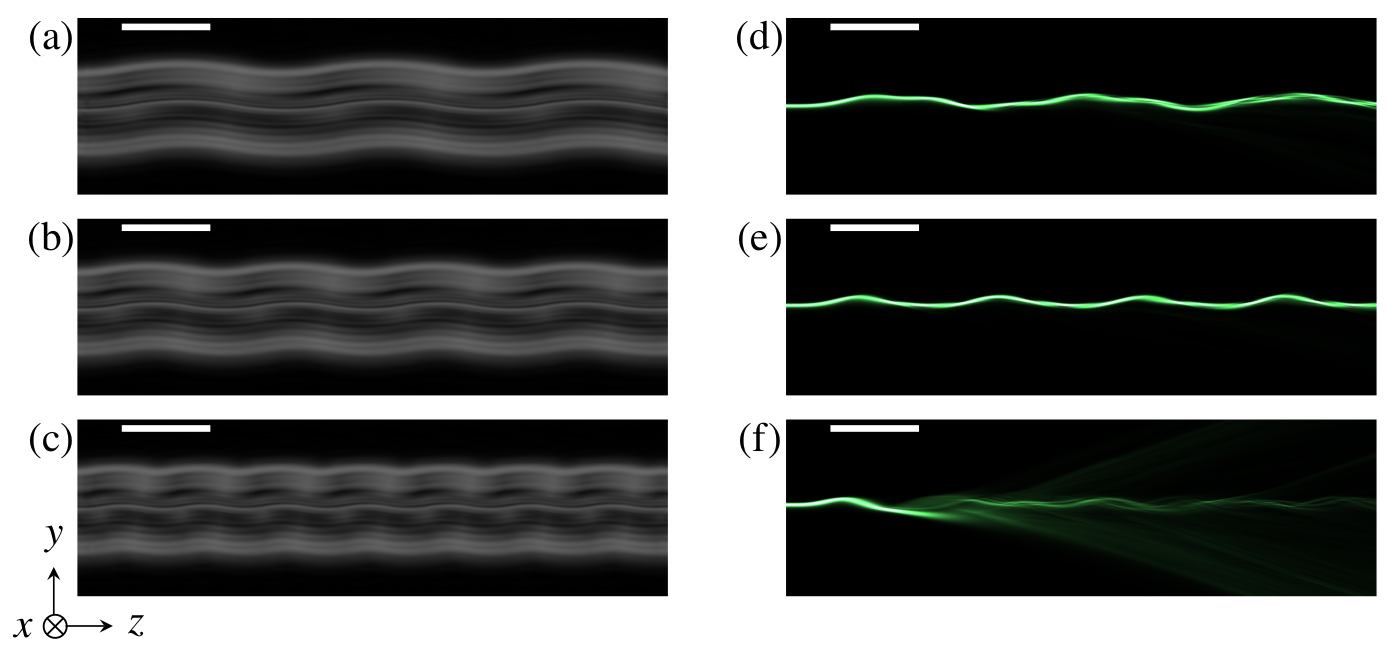
We present a unified theoretical framework for paraxial and wide-angle beam propagation methods in inhomogeneous birefringent media based on a minimal set of physical assumptions. The advantage of our schemes is that they are based on differential operators with a clear physical interpretation and easy numerical implementation based on sparse matrices. We demonstrate the validity of our schemes on three simple two-dimensional birefringent systems and introduce an example of application on complex three-dimensional systems by showing that topological solitons in frustrated cholesteric liquid-crystals can be used as light waveguides.

Download “Article” Physics_based_multistep_beam_propagation-1.pdf – Downloaded 181 times – 2 MB