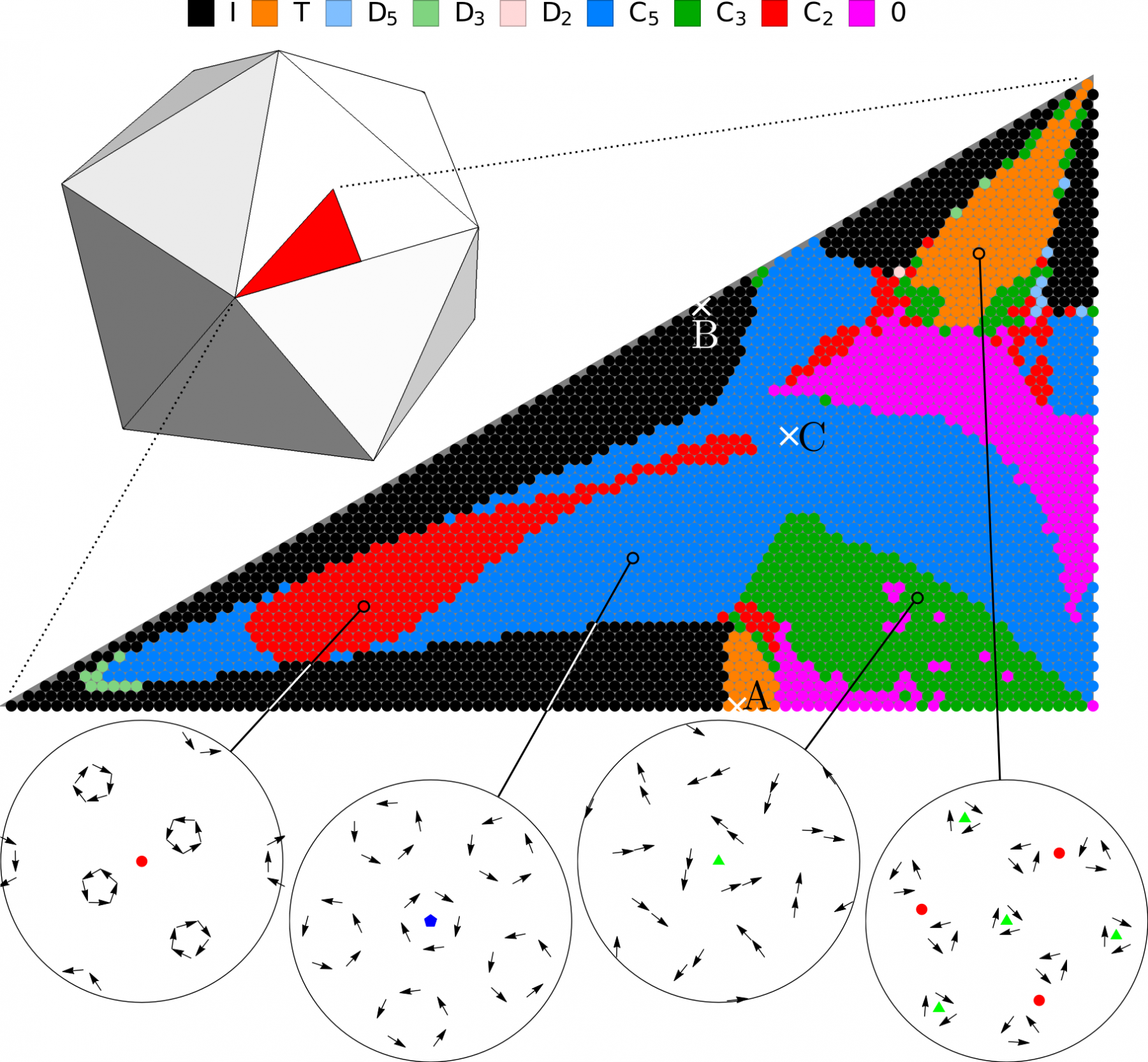
Anisotropic dipole-dipole interaction often plays a key role in biological, soft, and complex matter. For it to induce nontrivial order in the system, there must be additional repulsive interactions or external potentials involved that partially or completely fix the positions of the dipoles. These positions can often be represented as an underlying lattice on which dipole interaction induces orientational ordering of the particles. On lattices in the Euclidean plane, dipoles have been found to assume different ground-state configurations depending on the lattice type, with a global ordering in the form of a macrovortex being observed in many cases. A similar macrovortex configuration of dipoles has recently been shown to be the sole ground state for dipoles positioned on spherical lattices based on solutions of the Thomson problem. At the same time, no symmetric configurations have been observed, even though the positional order of Thomson lattices exhibits a high degree of symmetry. Here, we show that a different choice of spherical lattices based on Caspar-Klug construction leads to ground states of dipoles with various degrees of symmetry, including the icosahedral symmetry of the underlying lattice. We analyze the stability of the highly symmetric metastable states, their symmetry breaking into subsymmetries of the icosahedral symmetry group, and present a phase diagram of symmetries with respect to lattice parameters. The observed relationship between positional order and dipole-induced symmetry breaking hints at ways of fine-tuning the structure of spherical assemblies and their design.

Download “Article preprint” Symmetry_breaking_CasparKlug.pdf – Downloaded 172 times – 2 MB

Download a copy of the manuscript (preprint version)