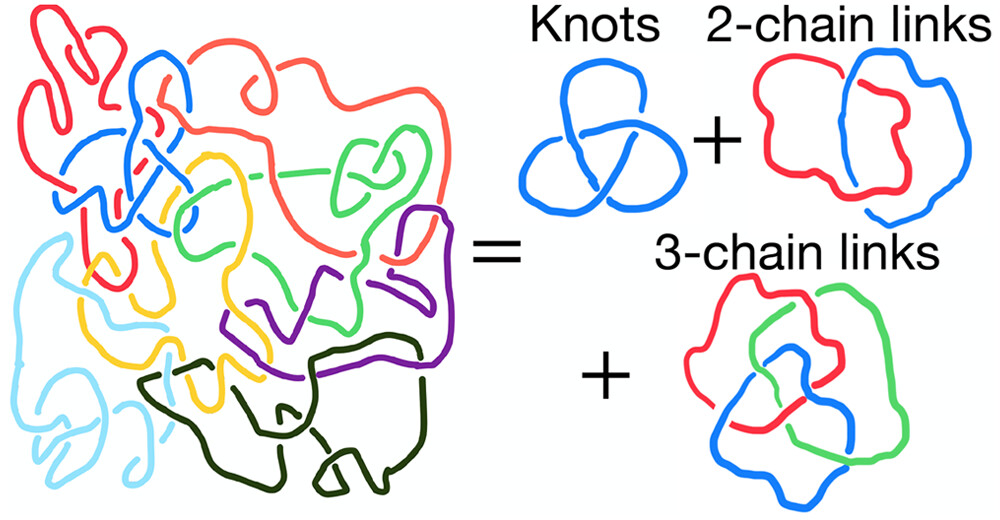
The viscous flow of polymer chains in dense melts is dominated by topological constraints whenever the single chain contour length, N, becomes larger than the characteristic scale Ne, defining comprehensively the macroscopic rheological properties of the highly entangled polymer systems. Even though the latter are naturally connected to the presence of hard constraints like knots and links within the polymer chains, the difficulty of integrating the rigorous language of mathematical topology with the physics of polymer melts has limited somehow a genuine topological approach to the problem of classifying these constraints and to how they are related to the rheological entanglements. In this work, we tackle this problem by studying the occurrence of knots and links in lattice melts of randomly knotted and randomly concatenated ring polymers of various bending stiffness. Specifically, by introducing an algorithm which shrinks the chains to their minimal shapes which do not violate topological constraints and by analyzing those in terms of suitable topological invariants, we provide a detailed characterization of the topological properties at the intra-chain level (knots) and of links between pairs and triplets of distinct chains. Then, by employing the Z1-algorithm on the minimal conformations in order to extract the entanglement length Ne, we show that the ratio N/Ne, the number of entanglements per chain, can be remarkably well reconstructed in terms of 2-chain links solely.

Download “Article preprint” recovery_of_entanglement.pdf – Downloaded 134 times – 2 MB

Download a copy of the manuscript (preprint version)