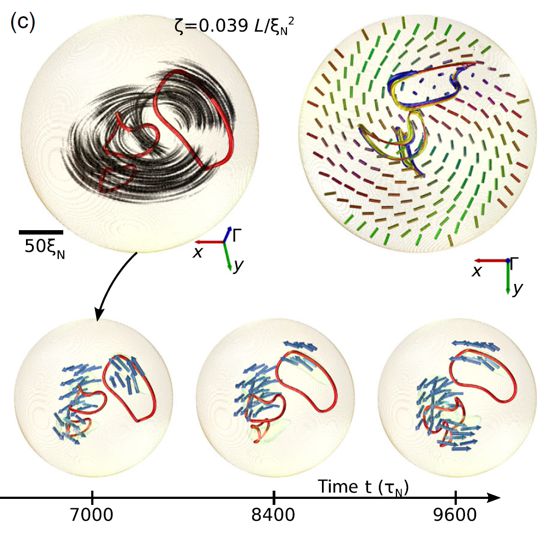
Active nematics contain topological defects that (under sufficient activity) move, create, and annihilate in a chaotic quasi-steady state, called active turbulence. However, understanding active defects under confinement is an open challenge, especially in three dimensions. Here, we demonstrate the topology of three-dimensional active nematic turbulence under the spherical confinement, using numerical modeling. In such spherical droplets, we show the three-dimensional structure of the topological defects, which,because of closed confinement, emerge in the form of closed loops or surface-to-surface spanning line segments. In the turbulent regime, the defects are shown to be strongly spatially and time varying, with ongoing transformations between positive winding, negative winding, and twisted profiles, and with defect loops of zero and nonzero topological charge. The timeline of the active turbulence is characterized by four types of bulk topology-linked events—breakup, annihilation, coalescence, and crossover of the defects—which we note could be used for the analysis of the active turbulence in different three-dimensional geometries. The turbulent regime is separated by a first-order structural transition from a low activity regime of a steady-state vortex structure and an offset single point defect. We also demonstrate coupling of surface and bulk topological defect dynamics by changing from strong perpendicular to in-plane surface alignment. More generally, this work aims to provide insight into three-dimensional active turbulence,distinctly from the perspective of the topology of the emergent three-dimensional topological defects.
Download a copy of the manuscript