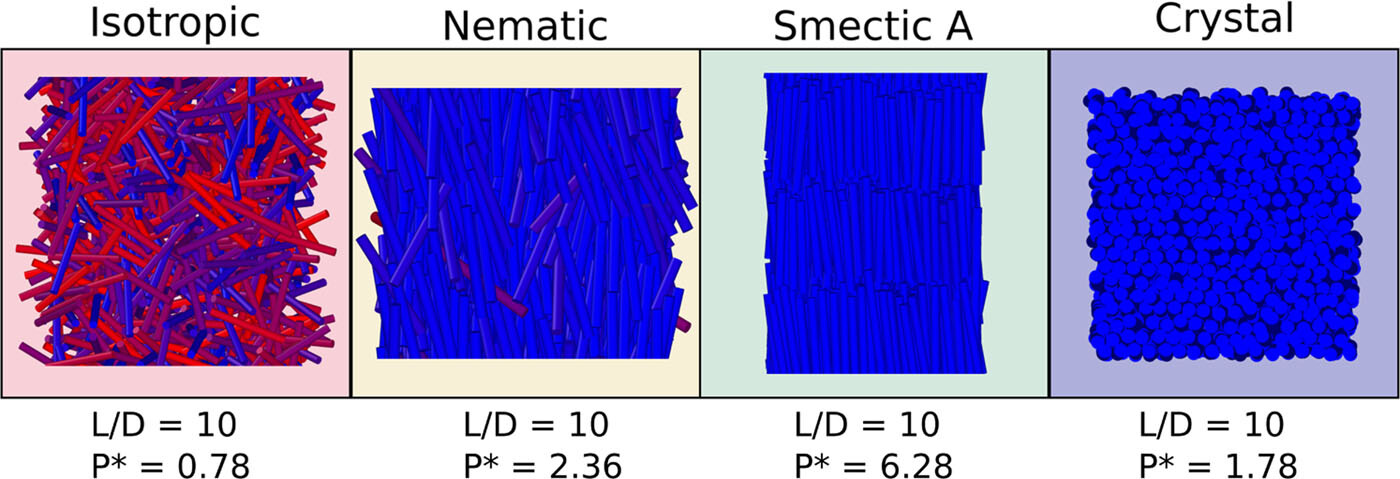
Using isobaric Monte Carlo simulations, we map out the entire phase diagram of a system of hard cylindrical particles of length L and diameter D, using an improved algorithm to identify the overlap condition between two cylinders. Both the prolate L/D>1 and the oblate L/D<1 phase diagrams are reported with no solution of continuity. In the prolate L/D>1 case, we find intermediate nematic N and smectic SmA phases in addition to a low density isotropic I and a high density crystal X phase, with I-N-SmA and I-SmA-X triple points. An apparent columnar phase C is shown to be metastable as in the case of spherocylinders. In the oblate L/D<1 case, we find stable intermediate cubatic Cub, nematic N, and columnar C phases with I-N-Cub, N-Cub-C, and I-Cub-C triple points. Comparison with previous numerical and analytical studies is discussed. The present study, accounting for the explicit cylindrical shape, paves the way to more sophisticated models with important biological applications, such as viruses and nucleosomes.

Download “Article preprint” phase_behaviour_hard_cylinders.pdf – Downloaded 166 times – 18 MB

Download a copy of the manuscript (preprint version)